编者按：为全面落实立德树人根本任务，学校以迎接新一轮本科教育教学审核评估为契机，加快推进我校人才培养质量保障体系建设，以评促建、以评促改、以评促管、以评促强。为深入开展迎评自建工作，评建办将持续推出审核评估巡礼系列活动，现开展省级一流本科课程系列展播专题，展示学校本科教育教学课程建设成果。

课程概述

（一）课程总体设计

《线性代数B》是辽宁科技学院理工科各专业的一门学科基础必修课，共40学时，2.5学分。它在自然科学、社会科学、工程技术、军事和工农业生产等领域中有广泛的应用。本课程的整体知识框架为主线思维和模块化相结合，课程围绕求解线性方程组的解这一主线和五个知识模块展开教学。本课程旨在使学生理解和掌握行列式、矩阵及其运算、向量的线性相关性、矩阵的初等变换与线性方程组、相似矩阵及二次型等理论及其有关知识。在教学过程中注重培养学生逻辑思维和抽象思维能力，提高学生分析问题解决问题的能力。通过本课程的学习，使学生具备有关线性代数的基本理论及方法，并能用它解决一些实际问题，为学生学习后续课程打下牢固的数学基础。

线性代数B课程总体设计图

（二）课程目标

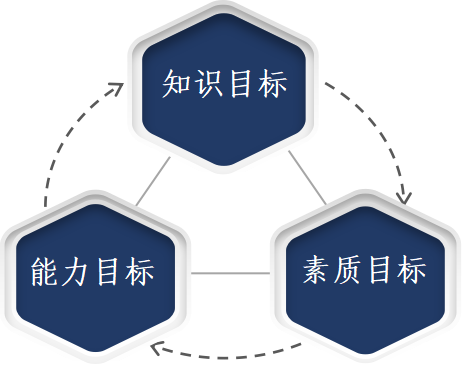
1.知识目标：学习线性代数的基本知识和基本理论，掌握常用的矩阵、行列式、线性方程组基本理论，掌握行列式的基本计算、系统掌握线性方程组解的结构及解法。

2.能力目标：通过向量的学习，掌握向量的空间结构和抽象概念，培养抽象思维能力和逻辑思维能力。通过线性代数的总体学习，提升学生运用数学方法分析和解决问题(包括实际问题和数学建模等)的能力，为学生未来的方向提供必要的数学基础和数学方法。

3.素质目标：在知识传授和能力培养过程中，培育学生的科学精神、探索创新精神，使学生能够自觉弘扬和践行社会主义核心价值观，不断增强“四个自信”，不断增强法治意识，引导学生深刻理解并自觉实践各行业的职业精神和职业规范。

课程建设历程

1.2018年《线性代数》课程首次尝试“N+2”过程考核，增加过程成绩占总成绩的比重，增加对学生平时学习的考核，促使学生加强平时学习，增加学生的表现机会，提升学生的创造性，以满足社会对应用型人才的需求。

2.2019年，为了满足各不同专业对《线性代数》课程内容的需求，《线性代数》课程实施模块化教学，分为《线性代数A》和《线性代数B》两个模块。

3.2020年，我们对“N+2”过程考核进一步优化，首次尝试将课程思政融入教学过程，探索课程思政建设的方法和途径。

4.2021年，进一步对课程进行课程思政方面的建设，使得课程思政融入整个教学的全过程，完成了从教学大纲、教学计划，到教案、教学课件的全方位的建设更新，最后形成《线性代数B》课程思政案例集。2021年，《线性代数B》被学校评为课程思政示范课。2021年，在辽宁科技学院学报发表论文1篇，题为“新工科建设背景下‘线性代数’课程教学内容改革实例”。

5.2022年，我们进行《线性代数B》试题库建设，并将试题库成功导入超星学习通平台，实施线上组卷、随机发卷、教考分离的考试模式。2022年，《线性代数B》被辽宁省评为线下一流课程。

6.2023年，根据工科专业的人才培养方案，进一步修订完善了《线性代数B》的教学大纲；进一步优化了教考分离的考试模式，完成了《线性代数B》的试卷库建设工作；进一步探寻课程思政的融入点，使课程思政更好地融入教学全过程。2023年，在辽宁科技学院学报发表论文1篇，题为“课程思政融入线性代数教学的探索与实践”。

7.2024年，进一步丰富了教案的内容，进一步完善了《线性代数B》的试卷库建设工作，并将钢铁精神、抗联精神和彰武治沙精神融入教学过程中，进一步完善了课程的课程思政建设。2024年，在辽宁科技学院学报发表论文1篇，题为“培根铸魂 润物无声——例谈线性代数教学中课程思政的实施”。

丛静老师的课堂

课程创新与特色

1.知识传授与价值引领相统一

课程团队根据课程特点和学生所在专业的专业特色，深入发掘该课程中所蕴含的思政教育元素，探寻课程思政融入点，把马克思主义哲学、中华传统数学文化、辽宁精神（钢铁精神、抗联精神、彰武治沙精神等）、国家建设与社会时政、生产生活实践等方面融入教学环节，引导学生树立正确的世界观和价值观，建立积极的人生观，坚定文化自信，传承科学精神，树立远大理想，厚植爱国情怀，培养创新意识，从而达到课程思政育人的目标。

2.显性教育和隐性教育相统一。

课题组既注重在授课过程中将专业知识教育与核心价值教育相融合，同时也通过自身的身体力行践行社会主义核心价值观，通过言传与身教并行，达到润物细无声的课程思政育人效果。充分利用教研室活动，鼓励团队教师创新探索，开展多种形式的课程思政研究与实践，坚持以每个课程思政元素为点，形成一门课的课程思政主线，形成这门课程的课程思政建设格局。

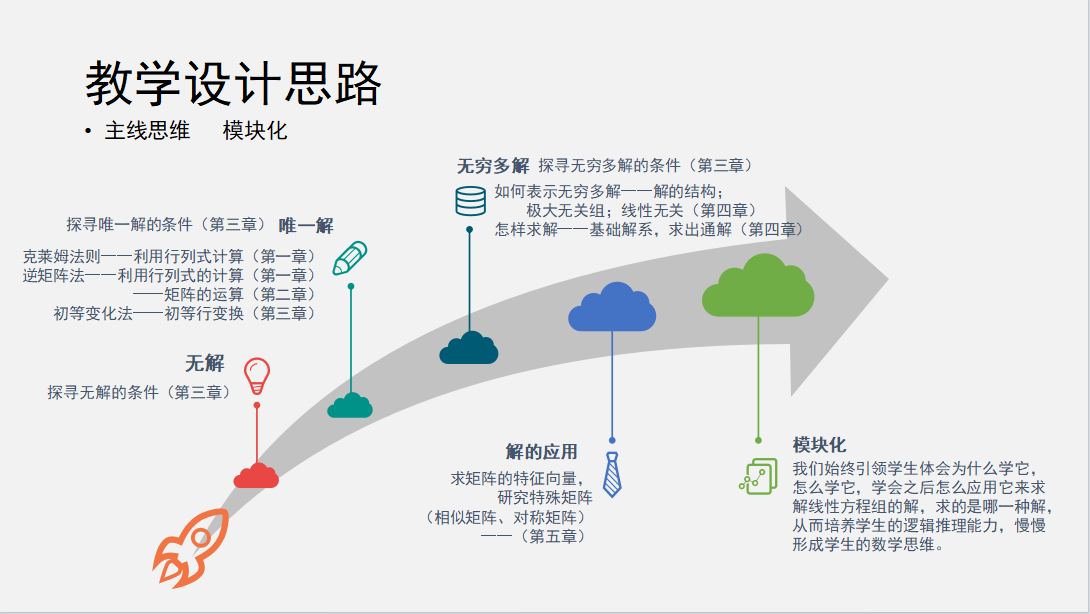
3.主线思维与模块化教学相结合

《线性代数B》这门课的整体知识框架我们采用主线思维和模块化相结合，这门课的主线是指求解线性方程组的解，模块是指五个部分的知识点各自为模块。这门课围绕的是求线性方程组的解这的一条主线，我们分析线性方程组的解的情况，即无解、唯一解和无穷多解三种情况，研究每一种情况存在的条件，探寻每种情况的求解方法，最后讨论解的用途。对于每一个模块，我们始终引领学生体会为什么学它， 怎么学它，学会之后怎么应用它来求解线性方程组的解，求的是哪一种解，从而培养学生的逻辑推理能力，慢慢形成学生的数学思维。

4.过程考核与结果考核相融合

构建多元化的课程评价体系，采用过程考核与结果考核相融合的评价方式，不仅评价学生的知识掌握程度，更重视学生的思想道德素质、社会责任感和实践能力的提升。过程考核实施全方位多元化考核体系，结果考核利用试卷库抽取期末考试试卷，实现了教考分离的考试模式。

丛静老师授课中

课程团队

（一）团队介绍

《线性代数B》这门课的课程负责人为基础部丛静老师，课程团队成员有王洪岩、戴志国、姜雄和李爽4位老师。丛静老师为理学硕士，副教授，现任辽宁科技学院基础部副主任，主要从事大学数学类课程的教学研究工作。

（二）课程建设及团队成果

1.主持相关课题1项。

项目列表

项目名称	承担人	批准 时间	批准单位	完成情况
基于三全育人的数学类课程“课程思政”建设	丛静	2023	辽宁科技 学院	在研

2. 发表相关论文3篇。

论文列表

论文题目	完成人	发表刊物或出版单位	发表时间
培根铸魂 润物无声——例谈线性代数教学中课程思政的实施	丛静	辽宁科技学院学报	2024.08
课程思政融入线性代数教学的探索与实践	丛静	辽宁科技学院学报	2023.12
新工科建设背景下“线性代数”课程教学内容改革实例	丛静	辽宁科技学院学报	2021.10

公开发表的论文

3.完成实用新型专利1项。

专利证书

4.赛教融合取得可喜成果。

教学团队钻研赛教融合渠道，指导学生参加大学生数学建模竞赛，取得优异成绩。

全国大学生数学建模竞赛获奖证书

5. 线性代数在教师教学大赛中获得一等奖。

线性代数获得教学大赛一等奖证书